KMeans：能從資料中找出 K 個分類的非監督式機器學習演算法

woff · 發表於 2021-6-1 21:33:04

使用 scikit-learn 與 Python

例子：

import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
# 隨機產生 10 組 2 features 的資料 500 筆 (dy 即原始目標值 label 0~9)
dx, dy = make_blobs(n_samples=500, n_features=2, centers=10, random_state=42)
# 用 KMeans 在資料中找出 5 個分組
kmeans = KMeans(n_clusters=5)
kmeans.fit(dx)
# 預測新的目標值 label
new_dy = kmeans.predict(dx)
plt.rcParams['font.size'] = 14
plt.figure(figsize=(16, 8))
# 以不同顏色畫出原始的 10 群資料
plt.subplot(121)
plt.title('Original data (10 groups)')
plt.scatter(dx.T[0], dx.T[1], c=dy, cmap=plt.cm.Set1)
# 根據重新分成的 5 組來畫出資料
plt.subplot(122)
plt.title('KMeans=5 groups')
plt.scatter(dx.T[0], dx.T[1], c=new_dy, cmap=plt.cm.Set1)
# 顯示圖表
plt.tight_layout()
plt.show()

複製代碼

KMeans 非監督式機器學習演算法 Python

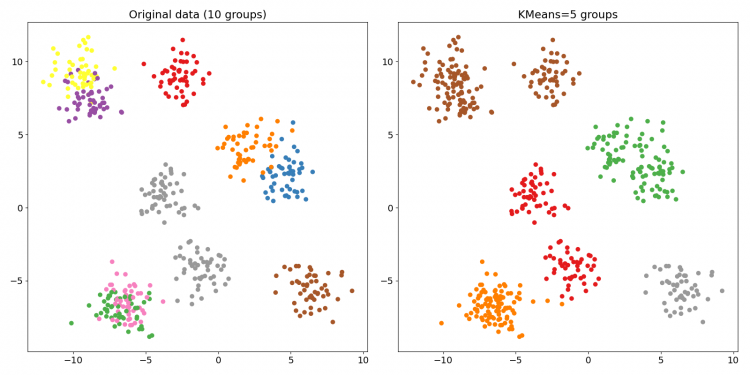
藉由顏色的識別，很容易看出資料從 10 組變成 5 組了。也就是說，你可以用 new_dy 取代原本的目標值 dy，等於是簡化了標籤數量。

上面之所以只有 2 個 features（即 2 個自變數），是因為這樣才能畫成二維圖表。增加到 3 個可畫成三維，來挑戰一下：

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D # matplotlib 3.2.0 後可省略
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
dx, dy = make_blobs(n_samples=500, n_features=3, centers=10, random_state=42)
kmeans = KMeans(n_clusters=5)
kmeans.fit(dx)
new_dy = kmeans.predict(dx)
plt.rcParams['font.size'] = 14
fig = plt.figure(figsize=(16, 8))
ax = fig.add_subplot(121, projection='3d')
plt.title('Original data (10 groups)')
ax.scatter(dx.T[0], dx.T[1], dx.T[2], c=dy, cmap=plt.cm.Set1)
ax = fig.add_subplot(122, projection='3d')
plt.title('KMeans=5 groups')
ax.scatter(dx.T[0], dx.T[1], dx.T[2], c=new_dy, cmap=plt.cm.Set1)
plt.show()

複製代碼

KMeans 非監督式機器學習演算法 Python

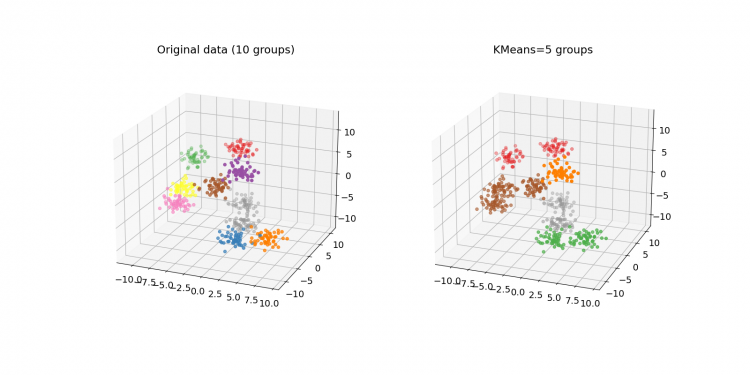
但 K 值要指定為多少才是合適的呢？說什麼非監督式學習，結果還不是要自己一個個試啊？特別是 make_blobs() 每次產生的資料還不一樣呢，一重新執行資料就跑掉了（除非你加上 random_state 參數來固定它）。

決定最佳 K 值的方式有幾種，scikit-learn 能做的有手肘法（看誤差平方和）和看側影係數。手肘法讓人有點無所適從，用側影係數比較簡單，找最大的值就行了。但這邊還是把兩者一併畫出來：

import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.metrics import silhouette_score
from sklearn.cluster import KMeans
colors = ['red', 'orange', 'yellow', 'green', 'cyan',
'blue', 'purple', 'brown', 'grey', 'black']
# 產生的資料組數 (10)
clusters = 10
# K 值的範圍 (2~10)
k_range = range(2, clusters + 1)
dx, dy = make_blobs(n_samples=500, n_features=2, centers=clusters, random_state=42)
distortions = []
scores = []
# 記錄每種 K 值建出的 KMeans 模型的成效
for i in k_range:
kmeans = KMeans(n_clusters=i).fit(dx)
distortions.append(kmeans.inertia_) # 誤差平方和 (SSE)
scores.append(silhouette_score(dx, kmeans.predict(dx))) # 側影係數
# 找出最大的側影係數來決定 K 值
selected_K = scores.index(max(scores)) + 2
# 重新建立 KMeans 模型並預測目標值
kmeans = KMeans(n_clusters=selected_K).fit(dx)
new_dy = kmeans.predict(dx)
# 新分組的資料中心點
centers = kmeans.cluster_centers_
plt.rcParams['font.size'] = 12
plt.figure(figsize=(12, 12))
# 原始資料分組
plt.subplot(221)
plt.title(f'Original data ({clusters} groups)')
plt.scatter(dx.T[0], dx.T[1], c=dy, cmap=plt.cm.Set1)
# 新資料分組
plt.subplot(222)
plt.title(f'KMeans={selected_K} groups')
plt.scatter(dx.T[0], dx.T[1], c=new_dy, cmap=plt.cm.Set3)
plt.scatter(centers.T[0], centers.T[1], marker='^', color='orange')
for i in range(centers.shape[0]): # 標上各分組中心點
plt.text(centers.T[0][i], centers.T[1][i], str(i + 1),
fontdict={'color': 'red', 'weight': 'bold', 'size': 24})
# 繪製誤差平方和圖 (手肘法)
plt.subplot(223)
plt.title('SSE (elbow method)')
plt.plot(k_range, distortions)
plt.plot(selected_K, distortions[selected_K - 2], 'go') # 最佳解
# 繪製係數圖
plt.subplot(224)
plt.title('Silhouette score')
plt.plot(k_range, scores)
plt.plot(selected_K, scores[selected_K - 2], 'go') # 最佳解
plt.tight_layout()
plt.show()

複製代碼

KMeans 非監督式機器學習演算法 Python

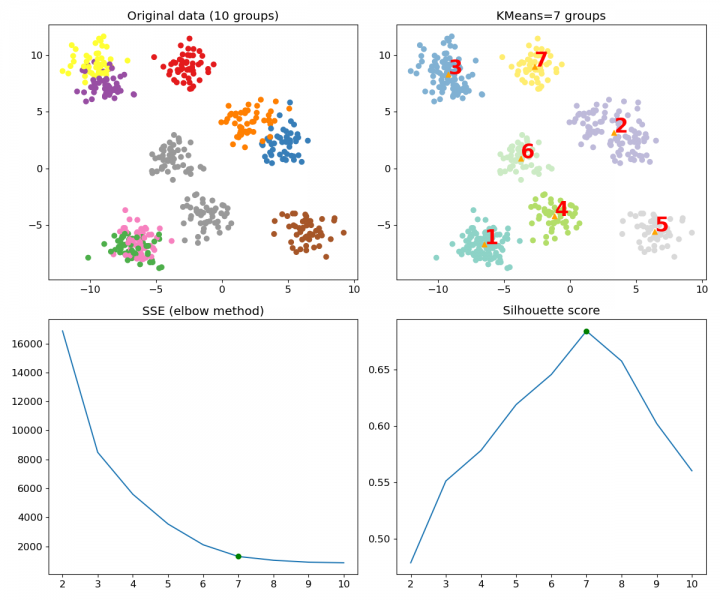
從上排的圖，可以看到資料自動從 10 組分成最佳的 7 組，比之前的 5 組合適多了，並標示出 KMeans 找到的各個中心點（來自 cluster_centers_）。下排的圖一邊是手肘法，另一邊是側影係數，兩者都在最佳 K 值處標上一個點。
當然，這邊我們在 make_blobs() 加入 random_state 參數，好確保每次產生的結果一致。你可以試著把這參數拿掉再重新執行程式，實際的 K 值和分組也會有所改變。這樣一來實際上會分成幾組，就看各組隨機資料彼此重疊的程度有多大。

那麼，KMeans 到底能怎麼套用在真實資料呢？考慮到 raw data 難尋，我們來嘗試對已經用到爛的波士頓房價資料集（原本是用來跑迴歸模型）做分析看看：

import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
from sklearn import datasets
from sklearn.metrics import silhouette_score
from sklearn.cluster import KMeans
data = datasets.load_boston()
# 把波士頓房價的 data 和 target 合併成一個 pandas DataFrame
dx = pd.DataFrame(data['data'], columns=data['feature_names'])
dy = pd.DataFrame(data['target'], columns=['MEDV'])
df = pd.concat((dy, dx), axis=1)
# 最大 K 值
K_max = 20
# 計算側影係數
scores = []
for i in range(2, K_max + 1):
scores.append(
silhouette_score(
df, KMeans(n_clusters=i).fit_predict(df)))
# 得出最佳 K 值
selected_K = scores.index(max(scores)) + 2
print('K =', selected_K, '\n')
# 對房價分組
kmeans = KMeans(n_clusters=selected_K)
labels = kmeans.fit_predict(df)
# 將分組資料 (分類標籤) 併入原資料
lb = pd.DataFrame(labels, columns=['labels'])
df = pd.concat((lb, df), axis=1)
# 印出標籤和房價、以及其統計結果
print(df[['labels', 'MEDV']], '\n')
print('原始資料\n', df['MEDV'].describe(), '\n')
# 抽出不同組的房價並印出統計結果
df_group = []
for i in range(selected_K):
df_new = df[df['labels']==i]['MEDV']
print(f'分類 {i + 1}\n', df_new.describe(), '\n')
df_group.append(df_new)
# 用 seaborn 畫出所有組別房價的箱型圖
sns.boxplot(data=df_group)
plt.show()

複製代碼

輸出結果：

K = 3
labels  MEDV
0       1  24.0
1       1  21.6
2       1  34.7
3       1  33.4
4       1  36.2
..    ... ...
501    1  22.4
502    1  20.6
503    1  23.9
504    1  22.0
505    1  11.9
[506 rows x 2 columns]
原始資料
count 506.000000
mean    22.532806
std       9.197104
min       5.000000
25%    17.025000
50%    21.200000
75%    25.000000
max    50.000000
Name: MEDV, dtype: float64
分類 1
count 366.000000
mean    24.931694
std       8.334857
min    11.800000
25%    19.500000
50%    22.800000
75%    28.575000
max    50.000000
Name: MEDV, dtype: float64
分類 2
count 102.000000
mean    17.429412
std       9.184539
min       5.000000
25%    12.150000
50%    15.300000
75%    20.600000
max    50.000000
Name: MEDV, dtype: float64
分類 3
count 38.000000
mean    13.126316
std    4.395310
min    7.000000
25%    9.750000
50%    13.250000
75%    14.975000
max    27.500000
Name: MEDV, dtype: float64

KMeans 非監督式機器學習演算法 Python

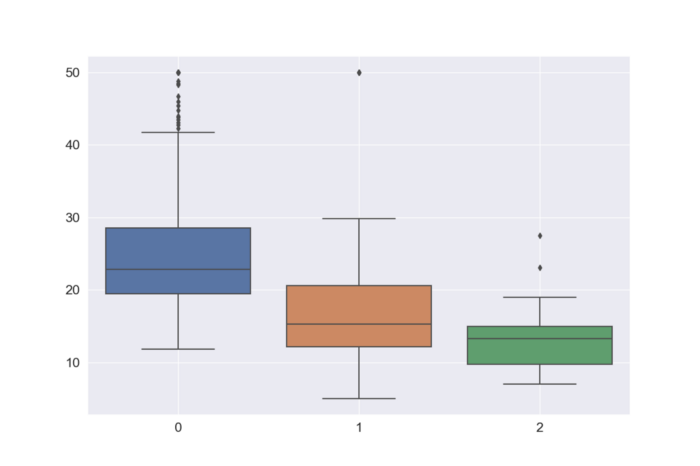
這裡 KMeans 把波士頓資料集分成了三組（就算把 K 上限設到 500 也一樣得到 K = 3），等於是加上了新的標籤。上面我們將這三組的房價拆開來看，可以發現每組的平均跟標準差都不同。當然，你程式跑出來這三組的統計數據可能會稍微有點差距就是。
這也許意味著，該資料集內的不動產依其居住條件（？）可大致劃分成三類。也許進一步分析資料集內的其他變數，會有更有趣的發現吧。
另一個常介紹的 KMeans 應用，便是圖片壓縮。更精確地說，是利用 KMeans 來減少顏色數量、進而達到減少圖片儲存空間的效果。

Photo by Simone Hutsch on Unsplash
下面的程式會從電腦載入一張照片（小編本人拍的照片，台北信義區，不算大的底片掃描檔，1272 x 1908），然後將它壓縮成只有 K 種顏色的圖片。

import numpy as np
import matplotlib.pyplot as plt # 需安裝 pillow 才能讀 JPEG
from matplotlib import image
from sklearn.cluster import MiniBatchKMeans
# K 值 (要保留的顏色數量)
K = 64
# 讀取圖片
image = image.imread(r'C:\Users\使用者名稱\Downloads\photo.jpg') / 255
w, h, d = tuple(image.shape)
image_data = np.reshape(image, (w * h, d))
# 將顏色分類為 K 種
kmeans = MiniBatchKMeans(n_clusters=K, batch_size=5000)
labels = kmeans.fit_predict(image_data)
centers = kmeans.cluster_centers_
# 根據分類將顏色寫入新的影像陣列
image_compressed = np.zeros(image.shape)
label_idx = 0
for i in range(w):
for j in range(h):
image_compressed[i][j] = centers[labels[label_idx]]
label_idx += 1
# 如果想儲存壓縮後的圖片, 將下面這句註解拿掉
#plt.imsave(r'C:\Users\使用者名稱\Downloads\compressed.jpg', image_compressed)
# 顯示原圖跟壓縮圖的對照
plt.figure(figsize=(12, 9))
plt.subplot(121)
plt.title('Original photo')
plt.imshow(image)
plt.subplot(122)
plt.title(f'Compressed to KMeans={K} colors')
plt.imshow(image_compressed)
plt.tight_layout()
plt.show()

複製代碼

在此，KMeans 從所有色彩（每個像素就有 256 x 256 x 256 種可能性）找出 K 種顏色，這時 cluster_centers_ 記錄的就是這 K 種顏色的紅綠藍組合。於是，只要根據新的標籤把分組過的顏色寫進新影像陣列，就能得到「壓縮過」的圖片了。
當然由於把整個照片讀進程式，電腦記憶體會爆掉，所以這邊改用 MiniBatchKMeans 來對像素「抽樣」。MiniBatchKMeans 跑得比 KMeans 快，但尋找中心點的效果也就會差一點。
下面來試試不同的 K 值，比較一下壓縮效果：

KMeans 非監督式機器學習演算法 Python

文章出處

賬號		自動登錄	找回密碼
密碼			註冊

[教學] KMeans：能從資料中找出 K 個分類的非監督式機器學習演算法

相關帖子

瀏覽過的版塊