卷積神經網路 CNN 的倒傳遞推導與稀疏矩陣觀點來看卷積計算

woff

卷積神經網路(Convolutional neural network, CNN)其他相關連結我也一起列上來

NN-2–1 卷積神經網路(Convolutional neural network, CNN) — 卷積運算、池化運算
NN-2–2 卷積神經網路(Convolutional neural network, CNN) — CNN運算流程
NN-2–3 卷積神經網路(Convolutional neural network, CNN):卷積計算的倒傳遞推導與稀疏矩陣觀點來看卷積計算
NN-2–4 卷積神經網路(Convolutional neural network, CNN):卷積計算中的步伐(stride)和填充(padding)
NN-2–5 卷積神經網路(Convolutional neural network, CNN): 1×1卷積計算在做什麼

這篇的重點在

1. 卷積計算的倒傳遞推導方式

2. 從稀疏矩陣(sparse matrix)觀點來看卷積計算

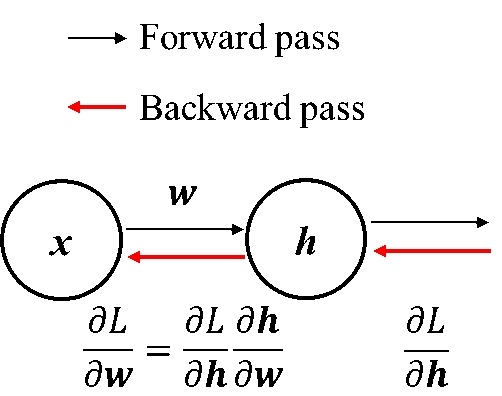
卷積計算的倒傳遞推導方式

卷積計算的forward pass和backward pass計算就如同一般MLP的倒傳遞計算方式一樣都是如下圖:

卷積神經網路 CNN 傳遞推導 稀疏矩陣 卷積計算

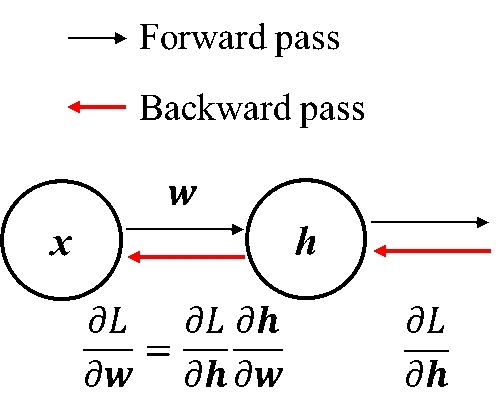
差別在於x部份與w部份，MLP在x部份通常是一個1D array的input，w則是全連結權重(fully connection)。

而在卷積計算(一般影像的卷積)部份:
x: 影像(2D array)
w: kernel map
h: output
卷積計算通常是實現局部連結(local connection)

這篇文張會舉一個影像大小是3*3，kernel map為2*2的例子來說明。

影像:

卷積神經網路 CNN 傳遞推導 稀疏矩陣 卷積計算

Kernel map:

卷積神經網路 CNN 傳遞推導 稀疏矩陣 卷積計算

Forward pass:

卷積計算，stride=1如下:

*: convolution

卷積神經網路 CNN 傳遞推導 稀疏矩陣 卷積計算

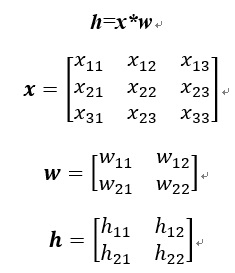
卷積神經網路 CNN 傳遞推導 稀疏矩陣 卷積計算

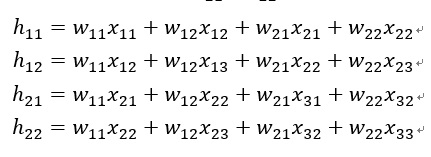
卷積神經網路 CNN 傳遞推導 稀疏矩陣 卷積計算

Backward pass:

卷積神經網路 CNN 傳遞推導 稀疏矩陣 卷積計算

因為這邊需要學習的參數是kernel map(w)內的元素(wij)，所以需要對卷積後的輸出和下一層的loss function(L)作偏微分(denote: ∂L / ∂w)，可以參考MLP那篇文章，然後因為∂L / ∂w無法直接計算，利用chain rule將其拆成兩項

卷積神經網路 CNN 傳遞推導 稀疏矩陣 卷積計算

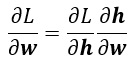
此時，∂L / ∂h和∂h / ∂w比較容易計算，如下:

卷積神經網路 CNN 傳遞推導 稀疏矩陣 卷積計算

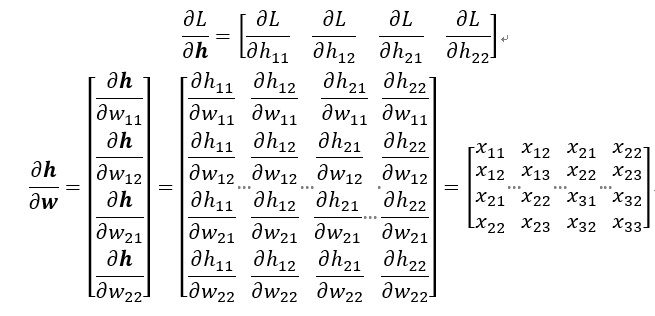
卷積神經網路 CNN 傳遞推導 稀疏矩陣 卷積計算

從稀疏矩陣觀點來看卷積計算Forward pass:

上述forward pass卷積的式子其實等價於兩個矩陣相成如下:

卷積神經網路 CNN 傳遞推導 稀疏矩陣 卷積計算

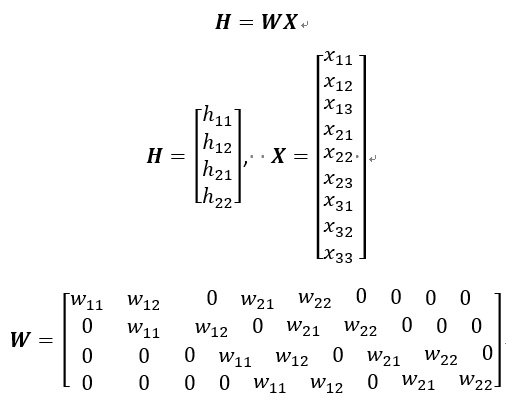
所以從這個式子來看其實卷積計算其實等價於一個MLP的一層，只是這個權重矩陣(W)為一個稀疏矩陣，而輸出層連結用到的概念是Local connected neural nets和權重共享(Shared Weight)的概念，權重在此範例只有4個(kernel map的元素)。

Note: 稀疏矩陣(sparse matrix)簡單說就是一個矩陣，裡面有很多元素都是0。

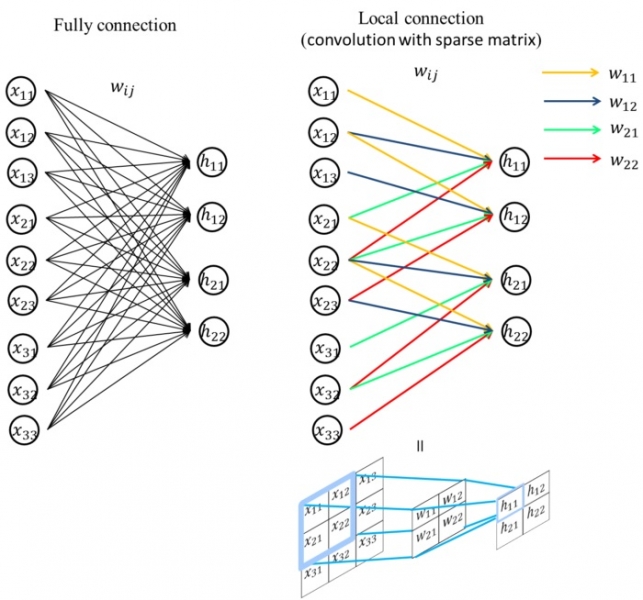
下圖是我做出來我覺得可以完整介紹為什麼是Local connection，左圖為「全連結」的連結方式，右圖為「區域連結」的連結方式

「全連結」的每個weight都是一個參數，此例共有9*4=36個參數
「區域連結」有權重共享的好處，此例則會只有4個參數。

卷積神經網路 CNN 傳遞推導 稀疏矩陣 卷積計算

Backward pass:

雖然local connection部份看起來很像full connection，但倒傳遞部份找解不是完全跟MLP一樣

Recall: 前面的backward pass結果

卷積神經網路 CNN 傳遞推導 稀疏矩陣 卷積計算

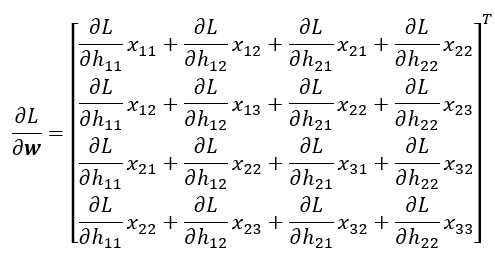
從上圖看到黃色的線(權重是w11)，在backward pass部份則是只看黃色線有連結到的部份

卷積神經網路 CNN 傳遞推導 稀疏矩陣 卷積計算

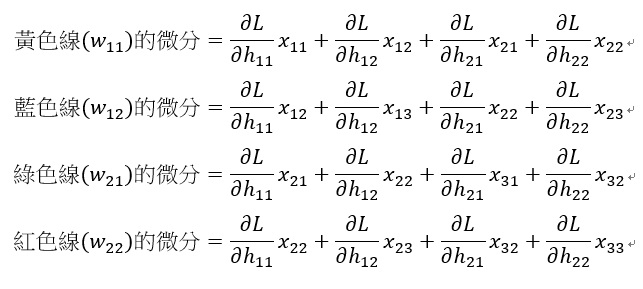
最後附上讓你看的不要不要的詳細推導: https://pdfs.semanticscholar.org/5d79/11c93ddcb34cac088d99bd0cae9124e5dcd1.pdf

文章出處